DEFINICIÓN
Las funciones exponenciales son las funciones que tienen la variable independiente x en el exponente, es decir, son de la forma:

El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Por ejemplo:
La ecuación anterior se cumple si los exponentes son iguales. Por tanto, en este ejemplo el valor que debe tomar x es 3.
Para conseguir igualdades como la anterior, tendremos que factorizar, expresar los números en forma de potencias, aplicar las propiedades de las potencias y escribir las raíces como potencias. En ocasiones, tendremos que realizar un cambio de variable para transformar la ecuación en una ecuación de primer o de segundo grado e, incluso, de grado mayor.
CARACTERÍSTICAS GENERALES
Las características generales de las funciones exponenciales son:
2) Su recorrido es (0, +∞) .
3) Son funciones continuas.
4) Como a0 = 1 , la función siempre pasa por el punto (0, 1).
La función corta el eje Y en el punto (0, 1) y no corta el eje X.
5) Como a1 = a , la función siempre pasa por el punto (1, a).
6) Si a > 1 la función es creciente.
Si 0 < a < 1 la función es decreciente.
7) Son siempre concavas.
8) El eje X es una asíntota horizontal.
Si a > 1 :
Al elevar un número mayor que 1 a cantidades negativas cada vez mas grandes, el valor de la potencia se acerca a cero, por tanto:
Ocurre lo contrario que en el caso anterior :
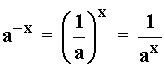
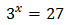
Podemos escribir 27 como la potencia . De este modo, la ecuación queda como
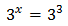
Tenemos una igualdad entre dos potencias con la misma base. Para que la igualdad sea cierta, ambas potencias deben tener el mismo exponente:
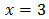
Al elevar un número mayor que 1 a cantidades negativas cada vez mas grandes, el valor de la potencia se acerca a cero, por tanto:
Cuando x → - ∞ , entonces a x → 0
- Si 0 < a < 1 :
Cuando x → + ∞ , encontes a x → 0
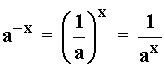
EJEMPLO 1:
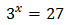
Podemos escribir 27 como la potencia . De este modo, la ecuación queda como
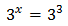
Tenemos una igualdad entre dos potencias con la misma base. Para que la igualdad sea cierta, ambas potencias deben tener el mismo exponente:
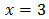
EJEMPLO 2:
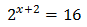
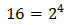
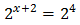
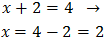
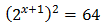
Escribimos 64 como una potencia de 2:
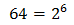
Operamos en la ecuación usando las propiedades de las potencias
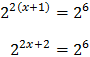
Por tanto, obtenemos una ecuación de primer grado:
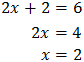
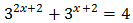
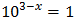
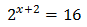
Escribimos 16 como una potencia de 2:
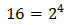
Podemos reescribir la ecuación como
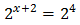
Por tanto, igualando los exponentes,
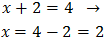
Luego la solución de la ecuación exponencial es x=2.
EJEMPLO 3:
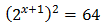
Escribimos 64 como una potencia de 2:
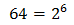
Operamos en la ecuación usando las propiedades de las potencias
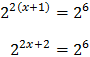
Por tanto, obtenemos una ecuación de primer grado:
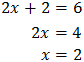
EJEMPLO 4:
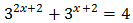
Reescribimos los sumandos:
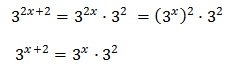
Con lo que podemos reescribir la ecuación como
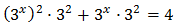
Sea el cambio de variable
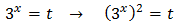
Sustituyendo en la ecuación obtenemos una ecuación de segundo grado
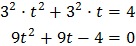
cuyas soluciones son
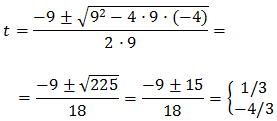
Por tanto, tenemos que
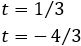
Al deshacer el cambio de variable,
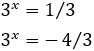
La segunda solución no es posible porque es negativa, pero la primera sí. Luego debe cumplirse
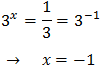
Por tanto, la solución de la ecuación exponencial es x = -1
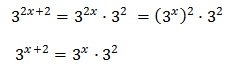
Con lo que podemos reescribir la ecuación como
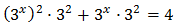
Sea el cambio de variable
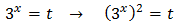
Sustituyendo en la ecuación obtenemos una ecuación de segundo grado
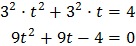
cuyas soluciones son
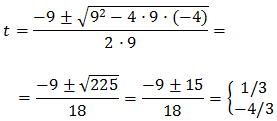
Por tanto, tenemos que
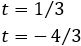
Al deshacer el cambio de variable,
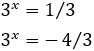
La segunda solución no es posible porque es negativa, pero la primera sí. Luego debe cumplirse
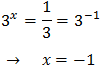
Por tanto, la solución de la ecuación exponencial es x = -1
EJEMPLO 5:
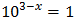
Podemos escribir 1 como una potencia de 10:
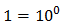
Con lo que podemos reescribir la ecuación como
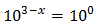
Por tanto, debe cumplirse
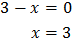
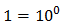
Con lo que podemos reescribir la ecuación como
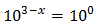
Por tanto, debe cumplirse
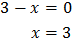
No hay comentarios.:
Publicar un comentario