Se llama función real de variable real a toda
función definida de un subconjunto D de los números reales, en el
conjunto R de los números reales, tal que a cada elemento x de D le
corresponde uno y sólo un elemento y de R:
Las relaciones y las funciones describen la interacción entre
variables que están ligadas. Estas relaciones incluyen valores independientes y entradas, que son las variables que pueden ser
manipuladas por las circunstancias. También incluyen valores dependientes y salidas, que son las variables determinadas por
los valores independientes. Existe otro par de componentes que debemos
considerar cuando hablamos de relaciones, se llaman dominio y rango.
El dominio de una función o relación es el conjunto de todos los
valores independientes posibles que una relación puede tener. Es la colección
de todas las entradas posibles.
El rango de una función o relación es el conjunto de todos los
valores dependientes posibles que la relación puede producir. Es la colección
de todas las salidas posibles.
de todos los valores que f toma.
EJEMPLOS:
Ejemplo 1:
Considere la función
mostrada en el diagrama.
Aquí, el dominio es el conjunto
{ A , B , C , E }. D no está
en el dominio, ya que la función no está definida para D .
El rango es el conjunto {1, 3, 4}. 2 no está en el
rango, ya que no hay letra en el dominio que se enlace con el 2.
Ejemplo 2:
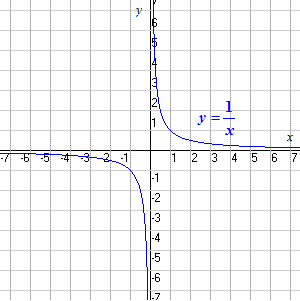
El dominio de la función
f ( x ) = 1/ x
es todos los números reales excepto el cero (ya que
en x = 0, la función no está definida: la división entre cero no está
permitida!).
El rango también es todos los números reales excepto
el cero. Puede ver que hay algún punto en la curva para cada valor
de y excepto para y = 0.
Ejemplo 3:
La notación siguiente muestra que el dominio de la
función está restringido al intervalo
(–1, 1).
f ( x ) = x 2 , –1  x
x  1
1
La gráfica de esta función es como se muestra. Dese
cuenta de los círculos abiertos, que muestran que la función no está definida
en x= –1 y x = 1. Los valores del rango de y desde 0
hasta el 1 (incluyendo el 0, pero no incluyendo el 1). Así el rango de la
función es
0  y < 1.
y < 1.
Ejemplo 4
Dominio
Puesto que se trata de una función polinómica (no
hay ningún punto problemático en la definición de la función, como dividir por
0), el dominio es todos los reales:
Dom(f)=R
Recorrido
Al ser un polinomio de primer grado, el recorrido es
todos los reales:
Im(f)=R
Ejemplo 5
Aquí hay una serie de figuras, cada una de ellas formada por cuadrados.

Podemos crear una función a partir de éstas usando el número de la figura como la entrada, y el número de cuadros que la conforman como la salida.
Una entrada de 1 tiene una salida de 1, ya que la figura 1 tiene sólo un cuadrado. Una entrada de 2 tiene una salida de 5, ya que la figura 2 contiene 5 cuadrados. Una entrada de 3, produce una salida de 9, ya que la figura 3 está formada de 9 cuadros. El dominio de ésta función se obtiene contando el número de entradas 1, 2, 3 que identifican cada una de las figuras usadas. Las entradas de ésta función son valores discretos, o valores que cambian en incrementos y no continuamente como la función del lanzamiento de la pelota. Sólo hay 3 figuras y por lo tanto las únicas posibles entradas son 1, 2, y 3. Entonces, el dominio de ésta función es 1, 2, 3. Podemos agrupar ésta lista de valores dentro de corchetes para indicar que forman un conjunto.
Dominio: {1, 2, 3}
El rango es el número de cuadros en cada figura. Las figuras tienen sólo 1, 5, o 9 cuadros, y ése es el rango. No hay ninguna figura que tenga 2 o 3.5 o cualquier otro número de cuadros. Como el dominio, el rango esta hecho de un conjunto de valores discretos.
Rango: {1, 5, 9}
Hemos limitado la entrada y la salida a 3 cada una porque sólo nos proporcionaron 3 figuras. ¿Cómo sería la notación del dominio y del rango si nos hubieran dicho que el patrón continuaría indefinidamente? ¡Fácil! Sólo añadimos tres puntos al final del conjunto de valores, para indicar que la secuencia continúa, así:
Dominio: {1, 2, 3, …}
Rango: {1, 5, 9, …}




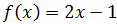
No hay comentarios.:
Publicar un comentario