Existen conectores u operadores logicos que nos permiten formar proposiciones compuestas (formadas por varias proposiciones). Los operadores logicos basicos son:
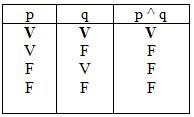Tabla de
verdad de la conjunción
Tabla de
verdad de la disyunción
Tabla de
Verdad Condicional
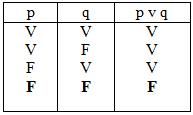Tabla de
Verdad Bicondicional
NEGACIÓN
La
negación es un operador que se ejecuta. sobre un único valor de
verdad, devolviendo el valor contradictorio de la proposición
considerada.
Se
simboliza generalmente por el signo "¬" y se lee “No es cierto
que …”
Tabla de
verdad de Negación
EJEMPLOS
DE NEGACION:
1.
p: “4 + 4 es igual a 9”
-p:
“4 + 4 no es igual a 9″
2.
p: “El 4 es un numero par”
-p:
“El 4 no es un numero par”
3.
p: "El pizarron es verde"
-p:
"El pizarron no es verde"
4.
p: "Jupiter es un planeta"
-p:
"Jupiter no es un planeta
5.
p: " Hoy es martes"
-p:
"Hoy no es martes"
CONJUNCION
La conjunción es
un operador que opera sobre dos valores de verdad, típicamente los valores de
verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando
ambas proposiciones son verdaderas, y falso en cualquier otro caso.
Es decir, es verdadera cuando ambas son verdaderas. El símbolo matemático
para la conjunción lógica varia en la literatura. Además de utilizar “Y”, el
símbolo en forma de es comúnmente utilizado para
la conjunción.
Tabla de
verdad de la conjunción
p ^ q
(se lee: ” p y q”)
EJEMPLOS
DE CONJUNCION:
1. p
= ” El numero 4 es par”
q =
”Siempre el residuo de los números pares es 2″
entonces…
p^q: “El
numero 4 es par y Siempre el residuo de los números pares
es 2″
2. p = ”
El numero mas grande es el 34”
q = ”El
triangulo tiene 3 lados″
entonces…
p^q: “El
numero mas grande es el 34 y El triangulo tiene 3 lados”
3. p=
"Esta lloviendo"
q=
"Esta nublado"
entonces...
p^q:
"Esta lloviendo y esta nublado
4. p=
"Trabajo mucho"
q=
"Gano un bajo sueldo"
entonces...
p^q:
"Trabajo mucho y gano un bajo sueldo"
5. p=
"Hoy es Lunes"
q=
"El dia esta soleado
entonces...
p^q:
" Hoy es lunes y el dia esta soleado"
DISYUNCION
Una disyunción
lógica, comúnmente conocida como O, o bien como , es un operador lógico que resulta
verdadero si cualquiera de los operadores es también verídico. El símbolo es la inicial de la
conjunción adversativa latina vel, que significa «o», «o bien».
La disyunción es
un operador que opera sobre dos valores de verdad, típicamente los valores de
verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando
una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando
ambas son falsas.
Tabla de
verdad de la disyunción
p v q (se
lee: ” p o q”)
EJEMPLOS
DE DISYUNCION:
1. p = ”
El numero 2 es par”
q = ” la
suma de 2 + 2 es 4″
entonces…
pvq: “El
numero 2 es par o la suma de 2 + 2 es 4″
2. p = ”
La raíz cuadrada del 4 es 2”
q = ” El
numero 3 es par″
entonces…
pvq:
“La raíz cuadrada del 4 es 2 o el numero 3 es par”
3. p=
"Puedes leer este articulo"
q=
"Puedes ediarlo"
pvq:
"Puedes leer este articulo o puedes editarlo"
4. p=
"La pluma es roja"
q=
"La pluma es azul"
pvq:
"La pluma es roja o azul
5. p=
"El vaso es bonito"
q=
"La leche esta dañada"
pvq:
"El vaso es bonito o la leche esta dañada"
CONDICIONAL
El condicional
material es un operador que opera sobre dos valores de verdad, típicamente
los valores de verdad de dos proposiciones, devolviendo el valor de
verdad falso sólo cuando la primera proposición es verdadera y la
segunda falsa, yverdadero en cualquier otro caso.
La condicional de
dos proposiciones p, q da lugar a la proposición; si p entonces q, se
representa por p → q
Tabla de
Verdad Condicional
EJEMPLOS
DE CONDICIONAL:
1. p:
“llueve”
q: “hay
nubes”
p→q: “Si llueve entonces hay
nubes”
2. p:
“Hoy es miércoles”
q: “Mañana
será jueves”
p→q: “Si Hoy
es miércoles entonces Mañana será jueves”
3. p:
"No llueve"
q:
"Iremos a la playa"
p→q:
"Si no llueve entonces iremos a la playa"
4. p:
"Gano la loteria"
q:
"Ire de viaje"
p→q:
"Si gano la loteria entonces ire de viaje"
5. p:
"Un cuadrilatero es un rectangulo"
q:
"Tiene cuatro ejes de simetria"
p→q:
"Si un cuadrilatero es un cuadrado entonces tiene cuatro
ejes de simetria"
BICONDICIONAL
El bicondicional o
doble implicación es un operador que funciona sobre dos valores de verdad,
típicamente los valores de verdad de dos proposiciones, devolviendo el valor de
verdad verdadero cuando ambas proposiciones tienen el mismo valor de
verdad, y falso cuando sus valores de verdad difieren.
Tabla de
Verdad Bicondicional
EJEMPLOS
DE BICONDICIONAL:
1. p:
“10 es un número impar”
q: “6 es
un número primo”
p↔q: “10
es un número impar si y solo si 6 es un número primo”
2. p:
“3 + 2 = 7”
q: “4 + 4
= 8”
p↔q: “3 +
2 = 7 si y solo si 4 + 4 = 8″
3. p:
"Puedes tomar el vuelo"
q:
"Compras un pasaje"
p↔q:
"Puedes tomar el vuelo si y solo si compras un pasaje"
4. p:
"Juan ingresa a la Universidad"
q:
"Juan estudia mucho"
p↔q:
"Juan ingresa a la Universidad si y solo si estudia mucho"
5. p:
"Luis obtiene el empleo "
q:
"Luis es graduado en quimica"
p↔q:
"Luis obtiene el empleo si y solo si es graduado en
quimica"
No hay comentarios.:
Publicar un comentario